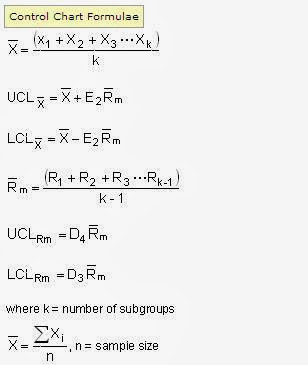I-MR Chart

I-MR Chart；這是Individuals and moving range charts的縮寫，也就是個別移動全距管制圖。

An I-MR chart, or individual and moving range chart, is a graphical tool that displays process variation over time. It signals when a process may be going out of control and shows where to look for sources of special cause variation.

(感謝匿名網友指正我們的錯誤 原個別移動平均管制圖 更正為 個別移動全距管制圖)

相關連結：個別值移動平均管制圖

Individuals and Moving-Range Charts

所謂Individuals and Moving-Range Charts ﹐我們稱之為X－Rm管制圖分析( X－Rm Control Chart)﹐應用在抽樣數為1 (每日一件 甚至每月一件等狀況) 之環境。

也有稱之為 I-MR Chart 的說法，與X－Rm管制圖分析( X－Rm Control Chart)說的是同一個管制圖。

X-Rm管制圖由個別值管制圖與移動全距管制圖組成

所謂移動全距為樣本值與前次樣本值之差﹐Ri = | Xi - X i-1|

相關管制界限的計算公式如下：

X-Rm管制圖乃X-bar R管制圖的延伸﹐其管制界限之計算不變﹐但n=2

因此下表中的 E2與D4 可分別計算查表 求出 E2 = 2.66, D4 =3.27





參考資料：
http://www.isixsigma.com/control_charts/individuals_and_moving_range_control_chart.asp
http://www.sqc.com.tw/Function/X-Rm.htm

平均數-全距管制圖 (X-bar R Chart) Excel 樣板

X-bar R管制圖可說是最常用的管制圖﹐我們特地整理了Excel樣板檔案﹐供網友們下載使用﹐期盼試用過的網友提供改正意見。

下載點：x'-R template

相關連結：平均數-全距管制圖 (X-bar R Chart)

EWMA Control Charts 指數加權移動平均管制圖

所謂指數加權移動平均 (Exponentially Weighted Moving Average (EWMA) ) 乃一監控製程之統計量﹐此統計量求取移動平均﹐並對越久的歷史資料給予越低的權重。

對於我們所熟悉的管制圖( Shewhart chart control ) ﹐其管制界限要定期更新﹐也就是說管制界限是根據最近的資料﹐用平均值加減三個標準差作為管制界限﹐而我們在此介紹的 EWMA 管制圖則不捨去過去的資料﹐但用較低的權重來計算管制界限。

在時間 t, 根據實際的觀測值（或量測值）我們可以求取 EWMAt如下：

EWMA_t = λY_t + ( 1-λ) EWMA_t-1 for t = 1, 2, ..., n.

• EWMA₀ 乃作圖前之歷史資料 (target)
• Y_t 乃 t 時間之量測值﹐Y_t-1 乃 t-1 時間之量測值
• n is the number of observations to be monitored including EWMA₀
• λ 值介於 0與 1 之間﹐表EWMA對於歷史量測值之權重係數﹐其值越接近1表對過去量測值的權重較低﹐我們所熟悉的管制圖( Shewhart chart control )其實是λ值等於1的特例。

EWMA的Variance可以下式求得：

s²_ewma = (λ/(2- λ)) s²

EWMA的管制界限計算：
UCL = EWMA₀ + ks_ewma
LCL = EWMA₀ - ks<sub>ewma (k值可以是3 或其他值）

範例：下面的例子﹐使用λ=0.3 依序求得EWMA之值如表


計算上表的 s = 1.97 EWMA=50 因此管制界限計算如下：
50 ±3 (0.3/1.7) (1.97x1.97)=50 ± 2.05 得管制圖如下：（EWMA處管制狀態下）</sub>


參考資料：
Engineering Statistics Handbook

平均數-全距管制圖 (X-bar R Chart)

註：為了便於電腦輸入﹐本站一律以X'代替X-bar﹐以X"代替X-bar-bar
平均數-全距管制圖﹐是針對計量型變數最常用的管制圖。
平均數-全距管制圖之製作：
收集數據﹐通常需要超過100個數據
將數據分組﹐通常以數據取得的時間﹑批量或製程條件分組﹐每組的數據數以2至5個為原則。
將數據記錄在記錄紙上﹐同時計算每個分組的X'與R﹐最後計算總體的X"與R'
計算X'之上管制界限：X' UCL = X" + A2R' (A2, D3, D4等值﹐參閱下表)
計算X'之下管制界限：X' LCL = X" - A2R'
計算R之上管制界限：R UCL = D4R
計算R之下管制界限：R LCL = D3R
繪製管制圖
寫下管制圖之相關資料﹐如製程取樣時間﹑操作機台﹑操作人員等。
管制界限常數表

其實管制界限就是3 sigma﹐但是過去計算工具不發達﹐乃作成上表﹐以查表方式方便計算
表中d2可用以推估製程之標準差﹐sigma = R'/d2(注意是製程標準差﹐而非X'標準差)　

相關連結：平均數-全距管制圖 (X-bar R Chart) Excel 樣板

管制圖異常警示(Out-of-control Signals)

管制圖作成後﹐吾人可根據圖上的趨勢﹐判斷是否有特殊因介入﹐使製程脫離統計之管制狀態(State of Statistical Control)。
西屋公司之異常警示原則(WECO rules)：參見下面的附圖
任一數據落在管制界限之外(與中線距離超過 3 sigma)
連續三點中的兩點落在 2 sigma之外 (與中線距離超過 2 sigma)
連續五點鐘的四點落在 1 sigma之外 (與中線距離超過 1 sigma)
連續九點在中線之同一側

Nelson Rules:
任一數據落在管制界限之外(與中線距離超過 3 sigma)
連續九點在中線之同一側
連續六點呈現上升或下降趨勢
連續十四點呈現鋸齒狀之升降趨勢
連續三點中的兩點落在 2 sigma之外 (與中線距離超過 2 sigma)
連續五點鐘的四點落在 1 sigma之外 (與中線距離超過 1 sigma)
連續十五點落在 1 sigma之內 (與中線距離少於 1 sigma)
連續八點都在 1 sigma 之外的上下兩側 (與中線距離超過 1 sigma)
參考資料：wikipedia

管制圖(Control Chart)

管制圖(Control Chart)是品管七大手法之一﹐可用以作為製程分析﹐亦可用以監控製程是否有異常(abnormality)發生。

作為製程分析用之管制圖﹐有時要將不同條件(如不同的原料來源)的製程﹐分別繪製管制圖﹐依據期間之差異﹐判定此不同條件對變易之影響之大小﹐藉以於確認製程變易的來源。

依變數之類型可分為計數型管制圖：
1.缺點數管制圖 (c chart)
2.平均缺點數管制圖 (u chart)
3.不良率管制圖 (p chart)
4.不良數管制圖 (np chart)

計量型管制圖　
1.個別值-全距管制圖 (X-R chart)
2.平均數-全距管制圖 (X bar-R Chart)
3.平均數-變異數管制圖 (X bar-s Chart)

等等 　 　

參考資料：
1. Guide to Quality Control (品質管理入門 石川 馨)
2.Seven Basic Quality Tools, Quality Tools,ASQ
3.Quality Tools

SPC, EPC

統計製程管制(Statistical Process Control, SPC)：透過統計知識﹐持續監控製程﹐藉此降低系統之變異﹐改善系統之品質之方法﹐謂之SPC。

工程製程管制(Engineering Process Control, EPC)﹐有稱為自動製程管制(Automatic Process Control, APC)：基本上是一種透過補償來改善品質的做法﹐應用在某些具有自動量測能力製程﹐透過自動量測之結果自動補償﹐藉此達到改善產品品質之目的。此法有其使用上的限制﹐通常應用在量測值有趨勢性的製程﹐例如自動車削作業﹐EPC可試著補償刀具之磨損值﹐使車削尺寸更接近設計中心值﹐同時也可延長刀具更換時間。